Adjusting Gait Timing with an ESP32-based Web Framework in MicroPython
I have been working on this for a while…
For the past two Summers I have been teaching a summer camp about “foldable robots”; I teach kids how to make mechanisms with folded cardboard and paper. By attaching RC servos, they can program their own motions and make unique, bio-inspired robots over the course of a week. The camp has grown well and I am working on refining the camp for younger students. This summer I taught students 13-17.
While students are easily inspired by nature, I struggle to get through the concepts of programming gaits from concept to implementation. I have been looking for a way to more easily help them investigate and identify workable walking gaits. Here is my progress so far.
What is the project?
I’ve created a little MicroPython-based project on that combines the following:
- An ESP32 microcontroller running MicroPython
- a basic RC servo class for converting position commands to a PWM signal
- the microdot web “micro” framework for serving a simple web app for controlling gait parameters
- The ability to work on either an existing wifi network or standalone as an access point.
The project can be found on Github. Here’s how to get it running:
- Install a code editor for working with the ESP32. I prefer VSCode with the Pymakr-preview plugin; Thonny is a rudimentary yet functioning alternative
- Flash micropython v1.20 or newer on to your ESP
- Open up the project and define an internet-connected wifi access point to connect to (for the first time).
- Upload the project to the microcvontroller and reset the ESP.
I have tutorials for each of these steps. Please reach out if you would like more details.
The ESP, when started up, will download a couple libraries from the internet and then soft reset itself. Once restarted, it will host a webpage at its ip address. You can use the page to control various aspects of the servos.
Once the libraries are downloaded, you can also reprogram the
boot.pyfile so that the ESP acts as its own wifi-access point.
I have provided a basic example with four servos. The schematic can be seen here:
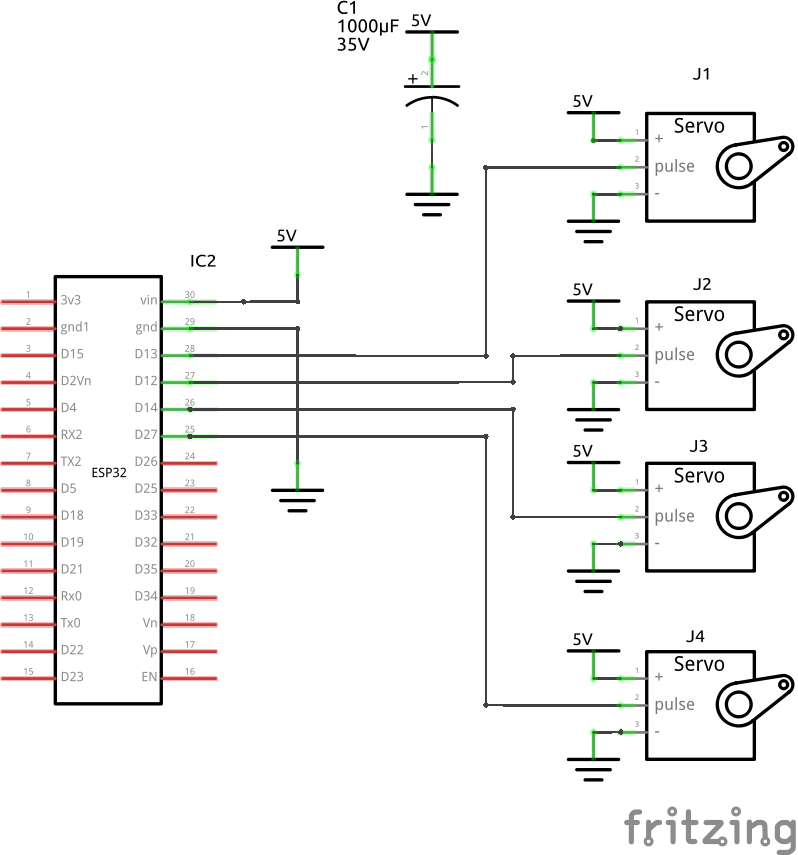
Schematic
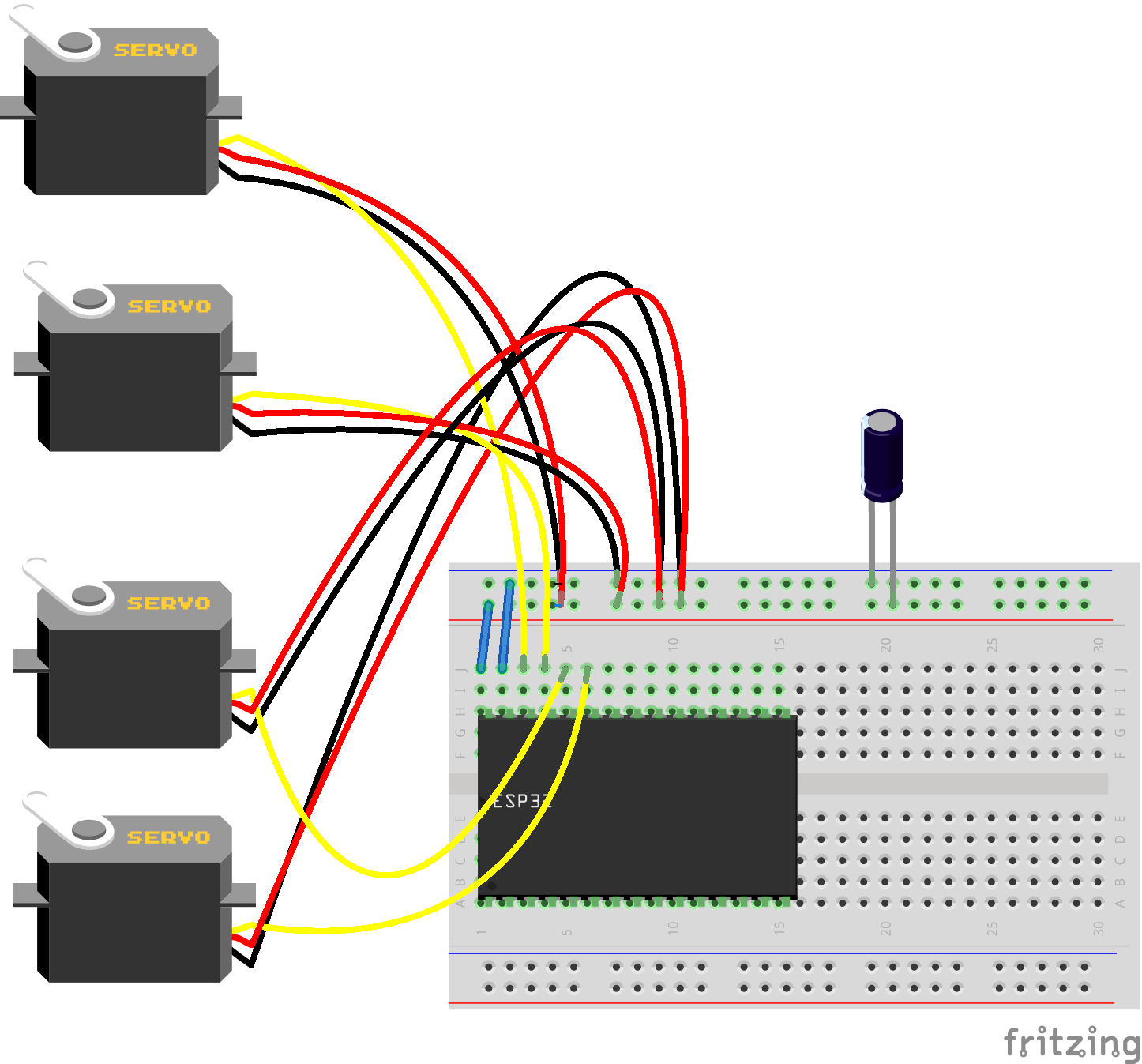
Breadboard
Sinusoidal Control
Each servo is controlled by the following equation
$\text{y}=A\sin\left(2\pi(ft-l_x)\right)+b$
where $y$ is the desired angle, $t$ is the current time in seconds, and the other variables in the expression correspond to the following adjustable parameters:
| Parameter | Meaning |
|---|---|
| $A$ | Amplitude |
| $f$ | frequency |
| $b$ | Y-offset |
| $l_x$ | Servo x time offset |
This gives you the ability to control the amplitude of your signal with $A$:
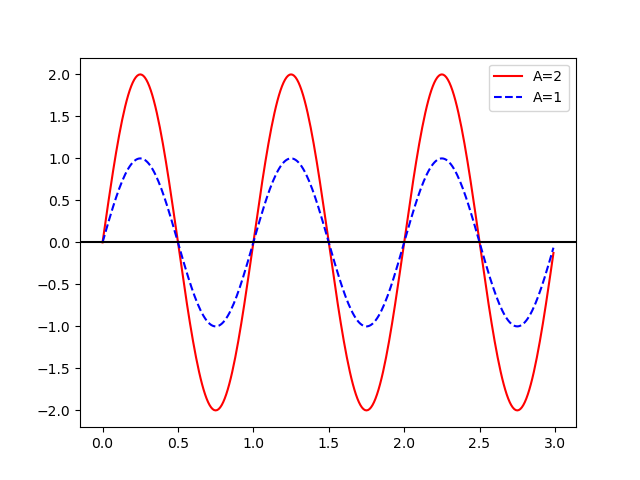
Amplitude
You can also change the frequency of your signal using $f$:
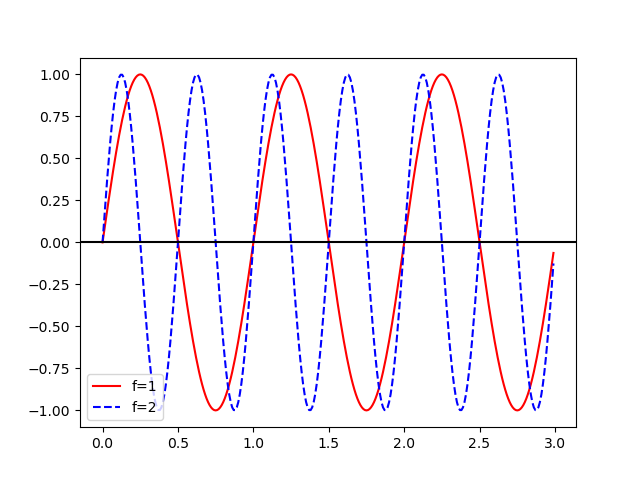
Frequency
You can shift the output of the desired output up or down with $b$
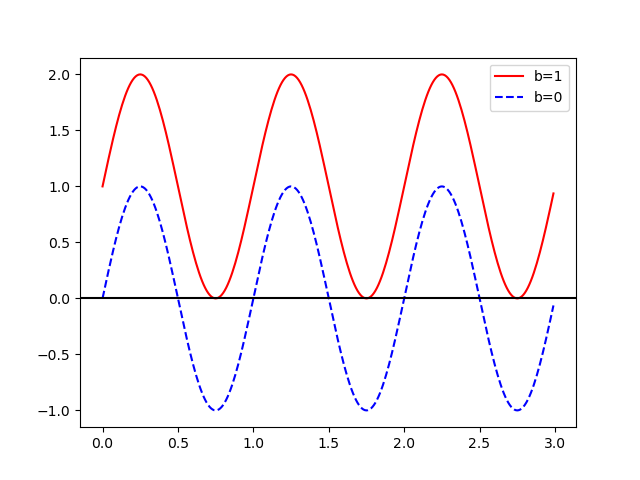
Y-Offset
You can also shift the timing of your signal by playing with $l_x$

Time Offset
Gaits
The time offset paramters, $l_x$, are specified in fractions of a full cycle. Thus, $l_x=0$ means the sinusoid crosses the x axis traveling in the positive direction at t=0, $l_x=0.5$ means the sinusoid is shifted in x by $\frac{f}{2}$ (crosses teh x axis traveling in the negative direction), and $l=1$ means your signal has wrapped around back to the beginning again. Thus, if you want to program a series of motors to be time-shifted in terms of fractions of a gait, you just have to play with the $l_x$ parameters to achieve very different results.
You can adjust all $l_1$, $l_2$, $l_3$, $l_4$ to be evenly distributed in time:

Four Servos
Or you can sequence two to be nearly on top of one another:
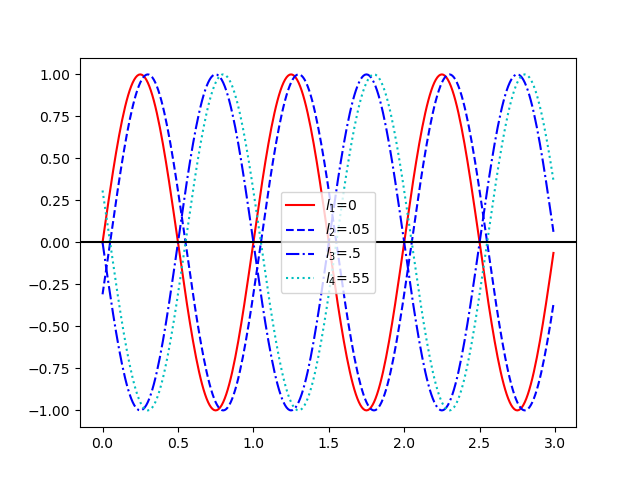
Different Timings